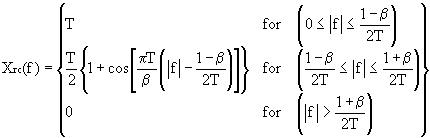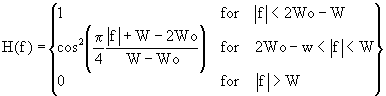Raised-Cosine (RC) and Root-Raised-Cosine (RRC) filters are commonly used in digital data modems. Here, we provide design formulas for these filters.
Notes:
- Each version of the same formula is algebraically equivalent; they just use different parameters.
- The impulse response formulas include a “sinc(x)” term, that is, “sin(x)/x”. Although “sinc(0)” seemingly includes a divide-by-zero, L’Hospital’s rule indicates that the numeric value of sinc(0) is 1.0. Therefore, whenever you find a sinc(0) condition in using these formulas, just substitute 1.0.
1. Raised Cosine Forumlas
1.1 Frequency Response
Version 1
Equation 9-2-26 of Digital Communications [Pro95]:
Definitions:
- f is the frequency.
- T is the symbol time.
- beta is the rolloff factor.
Version 2
Equation 2.74 of Digital Communications: Fundamentals and Applications [Skl88]:
Definitions:
- fis the frequency
- W – Wo is the excess bandwidth. (The rolloff factor is (W – Wo)/Wo.)
1.2 Impuse Response
Version 1
Equation 9-2-27 of Digital Communications [Pro95]:
Definitions:
- t is the time.
- T is the symbol time.
- beta is the rolloff factor.
Version 2
The following appears in the book Digital Communications: Fundamentals and Applications [Skl88]:
cos[2pi(W - Wo)t] h(t) = 2Wo(sinc 2WoT) ------------------- 1 - (4(W - Wo)t)^2( Note: The book is missing some parentheses in denomintor term which have been added here.)
Version 3
sin(bt) cos(at)
h(t) = ------- * ------------
bt 1-(2at/pi)^2
where b = 2 pi f
and a = 2 pi excess bandwidth.
2. Root-Raised Cosine Formulas
2.1 Frequency Response
Since the “root” aspect of a root-raised cosine filter is in the frequency domain, simply take the square root of the raised cosine frequency response given above to get the root-raised cosine frequency response.
2.2 Impulse Response
Version 1
Contributed by Clay S. Turner:
The RRC impulse response is given by: h(t) = pi^2 4at cos(t(a+b))+pi sin(t(b-a)) ----------- * ------------------------------ pi(a-b)-4a t(16t^2 a^2 - pi^2) where b= 2 pi f (f is usually half of your symbol rate) and a= 2 pi excess bandwidth
Version 2
Contributed by Jim Shima:
total taps in filter are N (odd) Ne = (N-1)/2 s = Ts/T k = index then, for n=0.. N let k = (n - Ne) (make causal) h(n) = T * sin[ pi * (r-1) * k * s] - 4 * r * Ts * k * cos[ pi*(r+1) * k*s] } -------------------------------------------------------------- T^(0.5) * pi * k * Ts * [ 16*r^2*k^2*s^2 - 1] 0/0 case: h(n) = T^(-0.5)* [ 1 - r*(1 - (4/pi)) ] must also take care of any x/0 cases.